RIOT -- The Convex Hull Problem: Detailed Description

Convex Hull

RIOT HOME

Convex Hull Instructions Details Demo Try It!

Solving with Graham Scan

To calculate the convex hull we use Graham's scan algorithm [G72]:

1. Find a point, P, interior to the convex hull by taking the average of the coordinates of all the given points.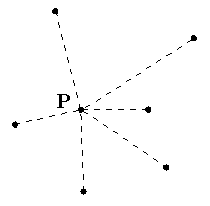

2. Translate the interior point, P, and all the others, so the interior point is at the origin.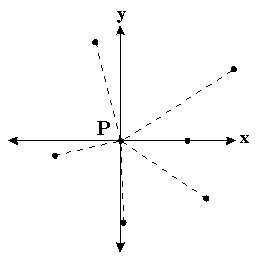

3. Find the angle between the line connecting P to each of the points and the X-axis. Sort the points according to the magnitude of the angle. This sorting determines the order that the algorithm will process the points.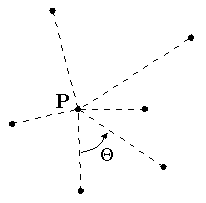

4. Starting from the lowest Y-axis coordinate, label the points P0, P1, ..., Pn.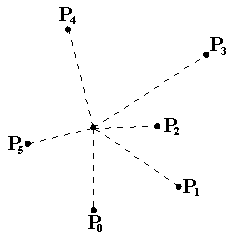

5. Let labels Pa, Pb, and Pc refer to P0, P1, and P2 respectively.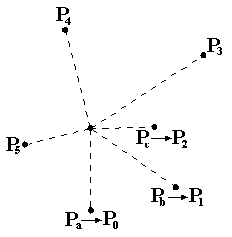

6. If the interior angle formed by Pa, Pb , Pc is greater than or equal to 180 degrees, then eliminate the point labeled with Pb. Point Pa becomes now point Pb. The predecessor of this point becomes point Pa. Otherwise, when there is no such predecessor as in the example here, the next point in the sequence, in this case P3, is added to form the new triplet as Pc, and the point previously labeled as Pc becomes Pb.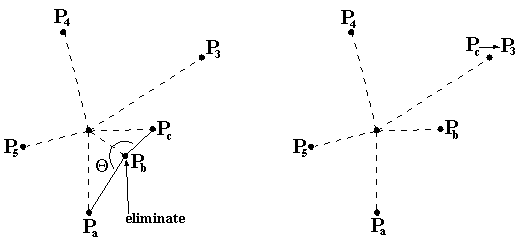

7. If the interior angle formed by the original Pa, Pb, Pc from before is less than 180 degrees, no points are eliminated and each of Pa, Pb, and Pc is advanced forward one point, in this case to points P1, P2, and P3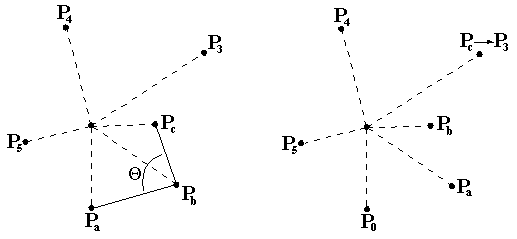

8. The algorithm continues by repeatinging steps 6 and 7 until Pb = P0. At this point, the algorithm stops and only the points of the convex hull remain.

References

[PS85] F. P. Preparata and M. I. Shamos Computational Geometry. Springer-Verlag,

New York (1985). pp. 107-110.

[G72] R.L. Graham, An efficient algorithm for determining the convex hull of a finite

planar set, Info. Proc. Lett. 1, 132-133 (1972).

[ Convex Hull | Instructions | Details | See a demo | Try It! ]